KMP与有限状态自动机

最近在学习字符串查找算法时，遇到了KMP算法，其中关于这块的介绍较为晦涩，记录一下自己的理解

字符串查找

字符串查找是一个应用非常多的功能，无论什么语言都会拥有该功能相关的一些周边函数或者概念，比如SQL。

通常来说，普通开发日常使用的时候，最简单的算法也就是暴力查找：

int M = pat.length(); // 需匹配的字符串
int N = txt.length(); // 原文本

for (int i = 0; i <= N - M; i++) {
    int j
    for (j = 0; j < M; j++) {
        if (txt.charAt(i + j) != pat.charAt(j)) break;
    }

    if (j == M) return i;
}

return -1;

这也是非常好理解的一种算法，将原文本中的每个字符都和匹配串的第一个字符进行比较，如果不匹配就去匹配下一个，如果匹配，则继续在匹配字符串中继续查找，直到匹配到末尾则是为成功。

这个算法可以直接达到目的，但是其中仍然有一些可以优化的地方，比如在字符串AABAABAAAA中查找字符串AABAAA时，当匹配到AABAAB的B时，则必然出现匹配失败，按照暴力算法的代码，则会回退到第二个A再次进行匹配，然而很明显，我们知道实际上完全不需要进行这么多的回退，KMP 算法则是为了解决该问题而出现的。

KMP算法

KMP算法网上大多也有介绍，基本上都是基于next[]来判断需要进行多少个字符的回退。

在Sedgewick的《Algorithms》一书中则使用了一种不太一样的计算方法，使得回退无需依赖于原字符串，而是仅仅使用匹配字符串就可以进行回退字符个数的预计，这就要归功于有限状态自动机

有限状态自动机

概念非常简单，就是记录在有限状态下，每个状态可以迁移到的0个或多个状态。简单来说，就类似于一种固定好的有向图，当给入一个属于字母表中的字符的时候，都可以按照预先定义好的状态，按照方向转移到下一个状态中，对应KMP算法则意味着回退到什么地方。

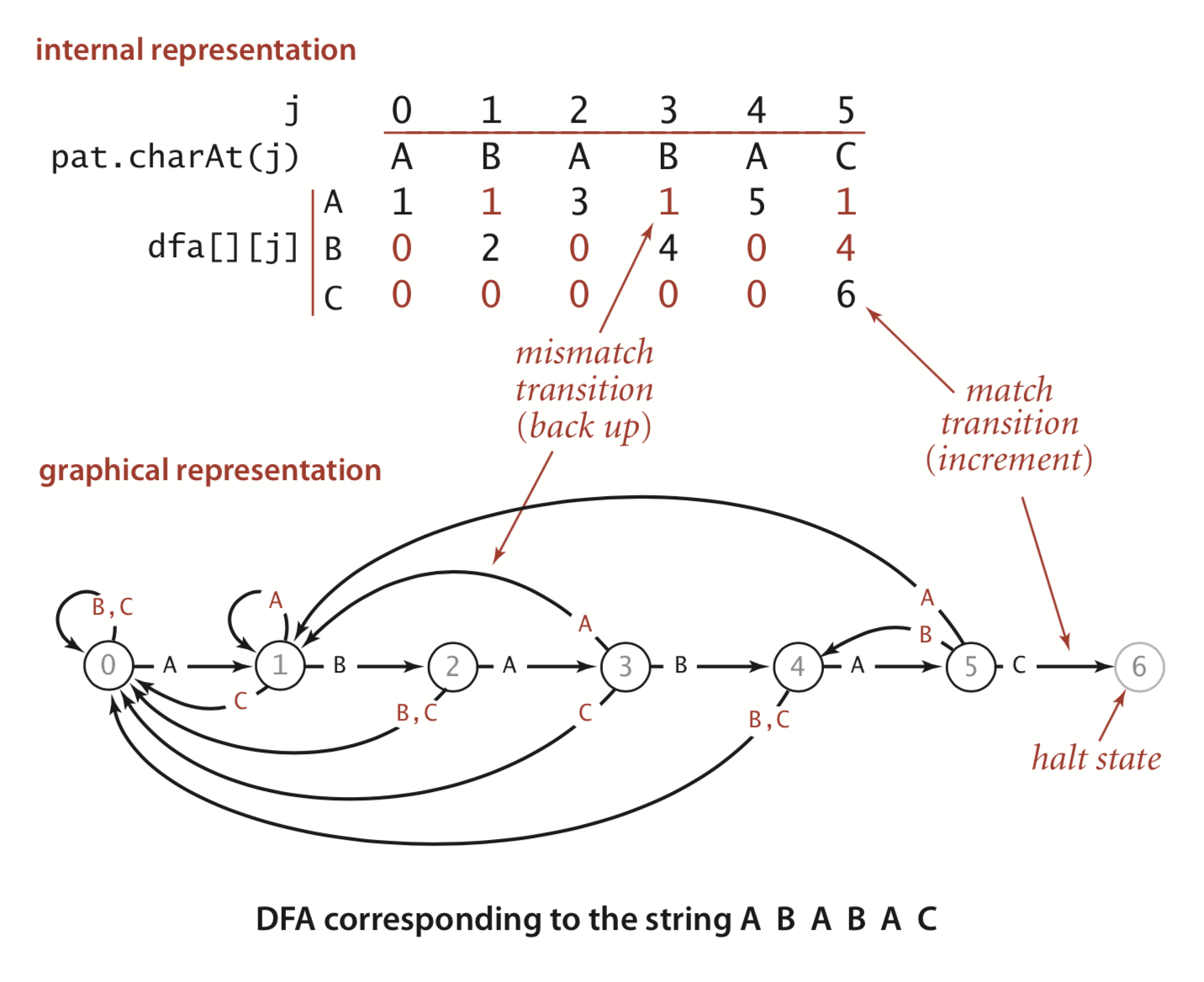
以图中为例，当匹配字符串为ABABAC时，有限状态机定义如下：

先暂定输入字母表为ABC三个字符

• 当输入A的时候，A被匹配到，状态机会认为其可以进行到状态1，输入另外两个则无法进行匹配，则为0

• 当再次输入A的时候，B则无法被匹配到，A字符的状态则被回滚到上个地方1，而输入B被匹配记录状态为2

• 再次输入A则又可以匹配到，此时的A会被记录状态为3，另外两个字符则还是会进行回退

• 当再次输入A的时候，B则无法被匹配到，A字符的状态则被回滚到上个地方1，而输入B被匹配记录状态为4

• 再次输入A则又可以匹配到，此时的A会被记录状态为5，另外两个字符则还是会进行回退

• 再次输入A和B的时候都无法被匹配到，A还是会回滚到1处，而B因为此时重启状态为3，则退回到4的位置

其中重启状态是个比较有意思的概念，就是需要回退到的状态，由于需要右移和忽略最后一个匹配失败，回退状态会在charAt(1)到charAt(j - 1)之间，也就是上一个可以达到的状态。

这种基于有限状态自动机的方式无需进行查找字符串中的回退，减少了消耗，是一种高效的查找算法